Резьба шаров и кристаллов из дерева
Фигурные звенья обычно выпиливают лобзиком из плоских заготовок: дощечек, реек, многослойной фанеры. Кроме соединения цепочки с помощью разлома, можно крупные звенья и распиливать, причем для фанеры последний способ обязателен. Нет необходимости во всех случаях распиливать соединяющие звенья на две части. Можно, например, выпилить с одной стороны звена кусочек для прохода других звеньев, а затем вклеить его. Тонкие пропилы лобзиком не создадут заметной помехи при стягивании кольца резинкой или шнуром.
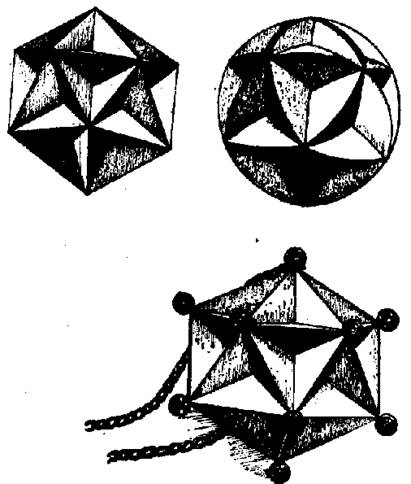
Рис. 18. Звездчатый кристалл (додекаэдр) и звездчатый шар, выполненные из заготовок одного размера. Звездчатый кристалл — женское украшение
Звездчатый кристалл «ежик» ввездчатый шар. Изображенный на рис. 18, а многогранник — малый звездчатый додекаэдр. Необыкновенно красивая симметричная форма многогранника делает его своеобразным декоративным украшением. Оригинальность многогранника-кристалла заключается в том, что его пятиконечные звезды имеют общие концы с такими , же соседними звездами. То есть, глядя на конец звезды, мы мысленно можем его связать с одной или со второй звездой, и так равномерно по всей поверхности кристалла. 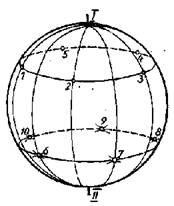
На первых порах пугает сложность изготовления такого многогранника, а вернее, сложность предстоящей разметки вершин и граней пятиконечных звезд. Однако разметка не так уж сложна, если в качестве исходной заготовки при выполнении кристалла в дереве использовать правильный шар. Тогда разбивку 12 вершин пятиконечных звезд можно представить следующим образом (рыс. 19): 2 вершины полюса на противоположных сторонах шара о по 5 вершин на двух поясах — параллелях шара. Именно уровень этих двух поясов, а значит, и их диаметр определяют успех дела: если разделить каждую параллель на 5 частей с целью получить положение 5 вершин звезд, то расстояния между ними должны быть такими же, как и расстояния каждой из них до первой вершины звезды, расположенной на полюсе. Заметим, что вершины звезд на параллели в нижней ча сти шара должны быть расположены не на одних меридианах с вершинами звезд на верхнем поясе, а строго между ними.
Сначала замерим длину экватора на шаровой заготовке, обогнув ее полоской бумага. Бела разделить полученную длину на коэффициент 5,86, то получится искомое расстояние между вершинами звезд на шаре. Теперь, взяв это расстояние циркулем, проведем в любом месте на его поверхности окружность, которая будет первым поясом — параллелью, и этим же размером циркуля разделим полученную окружность на 5 частей (центр окружности станет «северным полюсом»).
Определив вершины звезд в «северном полушарии», можно таким же способом найти положение вершив и в «южном полушарии». Однако мы не знаем места южного полюса. Конечно, его тоже можно построить, но проще из каждой точки деления ва первом поясе сделать ген же размером циркуля засечки в сторону второго пояса, го есть получить тем самым положение вершив звезд на втором поясе. А откладывая аз полученных точек все те же расстояния, можпо найти и другой полюс шара. Вероятно, из-за неточности коэффициента и самой шаровой поверхности мы получим при этом нс одну, а несколько точек, в центре которых и будет искомый полюс. Теперь, ведя построение в обратном направлении, .легко внести исправления допущенных погрешностей.
Дальнейшее выполнение звездчатого кристалла будет несложным: нужно вырезать трехгранные углубления между каждыми тремя смежными вершинами. Эти углубления формируют объемные концы пятиконечных звезд.
Но здесь могут быть два технических решения. Одно из них — сделать стенки трехгранного углубления плоскими, а ребра прямыми. Значит, следуя этому, решению, лучше сначала сделать между вершинами звезд плоские срезы шара. В этих плоскостях и будут лежать прямые линии — верхние ребра концов звезд. Таким образом мы превращаем шар в многогранник.
При выполнении трехгранных углублений будем ориентироваться на то, что вершина каждого такого углубления (пирамиды) находится посередине между вершинами звезд, то есть все грани одинаковы. А глубина выемки делается такой, что после выполнения всех пяти выемок вокруг вершины звезды должна образоваться общая единая плоскость, на которой лежит звезда.
Можно также сохранить линию каждого конца звезды как Дугу, лежащую на .поверхности шара. Для этого и стенки выемок придется делать не плоскими, а выпуклыми. Такую поделку скорее можно назвать звездчатым шаром (см. рисунок 18), чем кристаллом. Звездчатый шар смотрится более компактно, держит общую форму и больше подойдет в качестве составной детали композиции для таких изделий, как подвеска к люстре, нижняя часть стойки светильника и т. д. Фигурные шары со звездами выгодно использовать и для оформления вершин боковых колонн входной арки, например в пионерлагере.
Начинающему резчику легче справиться со звездчатым шаром, чем с кристаллом: прямые линии и плоскости в кристалле требуют большей точности. Общий ход работ по изготовлению звездчатого шара будет следующий. Сначала отрезают цилиндрическую заготовку, по высоте равную его диаметру. Обстругивают заготовку, придавая ей форму шара. Затем замеряют (циркулем, штангенциркулем) диаметр получен-. ного шара в самом узком месте, чтобы вырезать шаблон для проверки правильности формы шара этого диаметра. По шаблону подправляют ножом форму шара и размечают на его поверхности 12 вершин звезд. Точки-вершины накалывают шилом, чтобы не «потерять» их. Места, где будут проходить гребни лучей звезд, обрабатывают напильником и карандашом наносят линии гребней. Определив центры образовавшихся , треугольников, круглым резцом (стамеской) в центре треугольников делают предварительные углубления на необходимую глубину (на глаз) и вырезают соответствующие углубления с выпуклыми гранями.
При изготовлении звездчатого кристалла, конечно, необходимо предварительно переделать шар в многогранник.
